At What Rate Is The Exposed Surface Area Of The Water Changing When The Radius Is 2 Feet

4. Applications of Derivatives

iv.1 Related Rates

Learning Objectives

Express changing quantities in terms of derivatives.
Discover relationships among the derivatives in a given problem.
Use the chain dominion to observe the rate of change of i quantity that depends on the charge per unit of change of other quantities.

We have seen that for quantities that are changing over time, the rates at which these quantities change are given by derivatives. If two related quantities are changing over time, the rates at which the quantities alter are related. For example, if a balloon is being filled with air, both the radius of the balloon and the volume of the airship are increasing. In this section, nosotros consider several bug in which ii or more related quantities are changing and we written report how to determine the human relationship betwixt the rates of alter of these quantities.

Setting upward Related-Rates Problems

In many existent-globe applications, related quantities are changing with respect to time. For instance, if we consider the balloon example again, we can say that the rate of change in the book, $V$ , is related to the rate of change in the radius, $r$ . In this case, nosotros say that $\frac{dV}{dt}$ and $\frac{dr}{dt}$ are related rates because $V$ is related to $r$ . Here we study several examples of related quantities that are changing with respect to fourth dimension and we wait at how to calculate one rate of change given another rate of change.

Inflating a Balloon

Solution

The book of a sphere of radius $r$ centimeters is

$V=\frac{4}{3}\pi r^3 \, \text{cm}^3$ .

Since the balloon is beingness filled with air, both the volume and the radius are functions of time. Therefore, $t$ seconds subsequently beginning to fill up the balloon with air, the book of air in the airship is

$V(t)=\frac{4}{3}\pi [r(t)]^3 \, \text{cm}^3$ .

Differentiating both sides of this equation with respect to time and applying the chain dominion, we encounter that the rate of change in the volume is related to the rate of change in the radius by the equation

$V^{\prime}(t)=4\pi [r(t)]^2 \cdot r^{\prime}(t)$ .

The balloon is being filled with air at the constant rate of 2 cm^three/sec, so $V^{\prime}(t)=2 \, \text{cm}^3 / \sec$ . Therefore,

$2 \, \text{cm}^3 / \sec =(4\pi [r(t)]^2 \, \text{cm}^2) \cdot (r^{\prime}(t) \, \text{cm/sec})$ ,

which implies

$r^{\prime}(t)=\frac{1}{2\pi [r(t)]^2} \, \text{cm/sec}$ .

When the radius $r=3 \, \text{cm}$ ,

$r^{\prime}(t)=\frac{1}{18\pi} \, \text{cm/sec}$ .

What is the instantaneous rate of modify of the radius when $r=6 \, \text{cm}$ ?

Solution

$\frac{1}{72\pi} \, \text{cm/sec}$ , or approximately 0.0044 cm/sec

Before looking at other examples, let'southward outline the trouble-solving strategy we will be using to solve related-rates problems.

Problem-Solving Strategy: Solving a Related-Rates Trouble

Assign symbols to all variables involved in the problem. Draw a figure if applicable.
State, in terms of the variables, the information that is given and the rate to be determined.
Find an equation relating the variables introduced in step 1.
Using the chain rule, differentiate both sides of the equation institute in step 3 with respect to the independent variable. This new equation will relate the derivatives.
Substitute all known values into the equation from pace 4, then solve for the unknown rate of alter.

Note that when solving a related-rates problem, it is crucial not to substitute known values too soon. For example, if the value for a changing quantity is substituted into an equation before both sides of the equation are differentiated, and so that quantity will conduct as a constant and its derivative will not announced in the new equation institute in step 4. We examine this potential error in the following example.

Examples of the Procedure

Permit'due south now implement the strategy just described to solve several related-rates bug. The showtime instance involves a plane flying overhead. The relationship we are studying is between the speed of the plane and the charge per unit at which the distance betwixt the plane and a person on the ground is irresolute.

An Plane Flying at a Constant Top

An plane is flying overhead at a constant elevation of $4000$ ft. A man is viewing the plane from a position $3000$ ft from the base of a radio tower. The aeroplane is flying horizontally away from the human being. If the plane is flying at the rate of $600$ ft/sec, at what rate is the distance between the human and the plane increasing when the aeroplane passes over the radio tower?

Solution

Step 1. Describe a motion-picture show, introducing variables to stand for the different quantities involved.

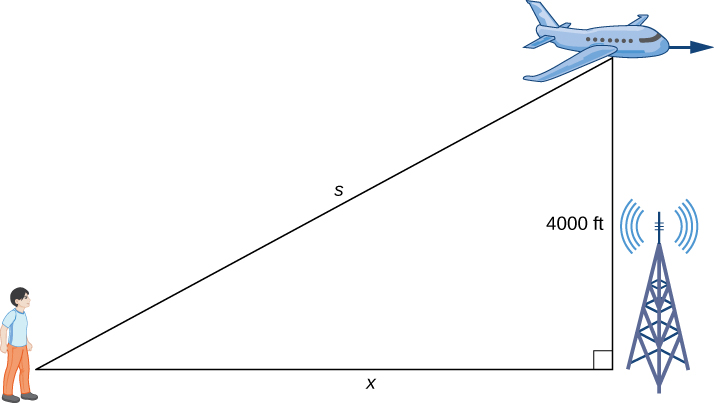
A right triangle is made with a person on the ground, an airplane in the air, and a radio tower at the right angle on the ground. The hypotenuse is s, the distance on the ground between the person and the radio tower is x, and the side opposite the person (that is, the height from the ground to the airplane) is 4000 ft.

An airplane is flight at a constant pinnacle of 4000 ft. The altitude between the person and the airplane and the person and the place on the ground direct beneath the airplane are changing. We announce those quantities with the variables $s$ and $x$ , respectively.

As shown, $x$ denotes the altitude between the homo and the position on the ground directly below the airplane. The variable $s$ denotes the altitude between the homo and the airplane. Note that both $x$ and $s$ are functions of time. We practise not introduce a variable for the elevation of the plane because it remains at a constant elevation of $4000$ ft. Since an object'south tiptop above the ground is measured as the shortest altitude between the object and the ground, the line segment of length $4000$ ft is perpendicular to the line segment of length $x$ anxiety, creating a right triangle.

Step 2. Since $x$ denotes the horizontal distance between the man and the point on the ground below the plane, $dx/dt$ represents the speed of the plane. We are told the speed of the plane is 600 ft/sec. Therefore, $\frac{dx}{dt}=600$ ft/sec. Since nosotros are asked to find the charge per unit of change in the distance between the human being and the plane when the plane is directly above the radio tower, we need to detect $ds/dt$ when $x=3000$ ft.

Pace 3. From the effigy, we tin can use the Pythagorean theorem to write an equation relating $x$ and $s$ :

$[x(t)]^2+4000^2=[s(t)]^2$ .

Step 4. Differentiating this equation with respect to time and using the fact that the derivative of a constant is aught, we arrive at the equation

$x\frac{dx}{dt}=s\frac{ds}{dt}$ .

Stride 5. Discover the rate at which the distance between the man and the plane is increasing when the airplane is straight over the radio belfry. That is, find $\frac{ds}{dt}$ when $x=3000$ ft. Since the speed of the plane is $600$ ft/sec, we know that $\frac{dx}{dt}=600$ ft/sec. We are not given an explicit value for $s$ ; however, since we are trying to detect $\frac{ds}{dt}$ when $x=3000$ ft, we can use the Pythagorean theorem to determine the distance $s$ when $x=3000$ and the height is $4000$ ft. Solving the equation

$3000^2+4000^2=s^2$

for $s$ , we have $s=5000$ ft at the fourth dimension of interest. Using these values, we conclude that $ds/dt$ is a solution of the equation

$(3000)(600)=(5000) \cdot \frac{ds}{dt}$ .

Therefore,

$\frac{ds}{dt}=\frac{3000 \cdot 600}{5000}=360$ ft/sec.

Note: When solving related-rates problems, it is important not to substitute values for the variables as well soon. For example, in stride three, we related the variable quantities $x(t)$ and $s(t)$ past the equation

$[x(t)]^2+4000^2=[s(t)]^2$ .

Since the plane remains at a constant acme, information technology is non necessary to innovate a variable for the elevation, and nosotros are immune to use the constant 4000 to denote that quantity. Nonetheless, the other two quantities are irresolute. If we mistakenly substituted $x(t)=3000$ into the equation before differentiating, our equation would accept been

$3000^2+4000^2=[s(t)]^2$ .

After differentiating, our equation would become

$0=s(t)\frac{ds}{dt}$ .

Every bit a outcome, nosotros would incorrectly conclude that $\frac{ds}{dt}=0$ .

What is the speed of the plane if the distance between the person and the plane is increasing at the rate of $300$ ft/sec?

Solution

$500$ ft/sec

We now render to the trouble involving the rocket launch from the showtime of the chapter.

Chapter Opener: A Rocket Launch

Solution

Step 1. Describe a picture introducing the variables.

Allow $h$ denote the height of the rocket above the launch pad and $\theta$ exist the angle between the photographic camera lens and the basis.

Step 2. We are trying to find the charge per unit of change in the angle of the camera with respect to time when the rocket is $1000$ ft off the ground. That is, we need to find $\frac{d\theta}{dt}$ when $h=1000$ ft. At that time, we know the velocity of the rocket is $\frac{dh}{dt}=600$ ft/sec.

Step iii. Now we need to find an equation relating the ii quantities that are changing with respect to time: $h$ and $\theta$ . How can we create such an equation? Using the fact that we have drawn a right triangle, information technology is natural to call back most trigonometric functions. Remember that $\tan \theta$ is the ratio of the length of the opposite side of the triangle to the length of the adjacent side. Thus, nosotros have

$\tan \theta =\frac{h}{5000}$ .

This gives u.s. the equation

$h=5000 \tan \theta$ .

Step 4. Differentiating this equation with respect to fourth dimension $t$ , we obtain

$\frac{dh}{dt}=5000 \sec^2 \theta \frac{d\theta}{dt}$ .

Pace 5. We want to detect $\frac{d\theta}{dt}$ when $h=1000$ ft. At this time, we know that $\frac{dh}{dt}=600$ ft/sec. We need to determine $\sec^2 \theta$ . Think that $\sec \theta$ is the ratio of the length of the hypotenuse to the length of the adjacent side. Nosotros know the length of the next side is $5000$ ft. To determine the length of the hypotenuse, we utilise the Pythagorean theorem, where the length of i leg is $5000$ ft, the length of the other leg is $h=1000$ ft, and the length of the hypotenuse is $c$ anxiety as shown in the following figure.

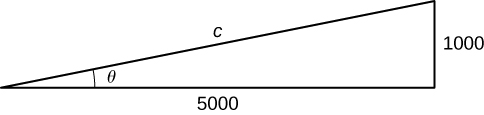
A right triangle has one angle with measure θ. The hypotenuse is c, the side length opposite the angle with measure θ is 1000, and the side adjacent to the angle with measure θ is 5000.

We run into that

$1000^2+5000^2=c^2$

and nosotros conclude that the hypotenuse is

$c=1000\sqrt{26}$ ft.

Therefore, when $h=1000$ , nosotros have

$\sec^2 \theta =(\frac{1000\sqrt{26}}{5000})^2=\frac{26}{25}$ .

Recall from step iv that the equation relating $\frac{d\theta}{dt}$ to our known values is

$\frac{dh}{dt}=5000 \sec^2 \theta \frac{d\theta}{dt}$ .

When $h=1000$ ft, we know that $\frac{dh}{dt}=600$ ft/sec and $\sec^2 \theta =\frac{26}{25}$ . Substituting these values into the previous equation, we make it at the equation

$600=5000(\frac{26}{25})\frac{d\theta}{dt}$ .

Therefore, $\frac{d\theta}{dt}=\frac{3}{26}$ rad/sec.

What rate of change is necessary for the elevation bending of the camera if the camera is placed on the footing at a distance of $4000$ ft from the launch pad and the velocity of the rocket is $500$ ft/sec when the rocket is $2000$ ft off the basis?

Solution

$\frac{1}{10}$ rad/sec

In the adjacent example, we consider water draining from a cone-shaped funnel. We compare the rate at which the level of water in the cone is decreasing with the rate at which the volume of h2o is decreasing.

H2o Draining from a Funnel

Water is draining from the bottom of a cone-shaped funnel at the rate of $0.03 \, \text{ft}^3 /\text{sec}$ . The height of the funnel is $2$ ft and the radius at the top of the funnel is $1$ ft. At what rate is the height of the water in the funnel changing when the tiptop of the water is $\frac{1}{2}$ ft?

Solution

Stride 1: Depict a motion picture introducing the variables.

Let $h$ denote the elevation of the water in the funnel, $r$ announce the radius of the water at its surface, and $V$ denote the book of the water.

Pace two: We demand to determine $\frac{dh}{dt}$ when $h=\frac{1}{2}$ ft. We know that $\frac{dV}{dt}=-0.03 \text{ft}^3 / \text{sec}$ .

Step 3: The book of water in the cone is

$V=\frac{1}{3}\pi r^2 h$ .

From the figure, nosotros see that nosotros have similar triangles. Therefore, the ratio of the sides in the two triangles is the same. Therefore, $\frac{r}{h}=\frac{1}{2}$ or $r=\frac{h}{2}$ . Using this fact, the equation for volume can exist simplified to

$V=\frac{1}{3}\pi (\frac{h}{2})^2 h=\frac{\pi}{12}h^3$ .

Stride 4: Applying the chain dominion while differentiating both sides of this equation with respect to fourth dimension $t$ , nosotros obtain

$\frac{dV}{dt}=\frac{\pi}{4}h^2 \frac{dh}{dt}$ .

Stride 5: We desire to find $\frac{dh}{dt}$ when $h=\frac{1}{2}$ ft. Since water is leaving at the rate of $0.03 \, \text{ft}^3 / \text{sec}$ , nosotros know that $\frac{dV}{dt}=-0.03 \, \text{ft}^3 / \text{sec}$ . Therefore,

$-0.03=\frac{\pi}{4}(\frac{1}{2})^2 \frac{dh}{dt}$ ,

which implies

$-0.03=\frac{\pi}{16}\frac{dh}{dt}$ .

It follows that

$\frac{dh}{dt}=-\frac{0.48}{\pi}=-0.153$ ft/sec.

At what rate is the height of the water changing when the height of the water is $\frac{1}{4}$ ft?

Solution

$-0.61$ ft/sec

Key Concepts

To solve a related rates trouble, showtime draw a picture that illustrates the human relationship between the ii or more related quantities that are irresolute with respect to time.
In terms of the quantities, country the information given and the rate to exist found.
Find an equation relating the quantities.
Apply differentiation, applying the concatenation rule as necessary, to find an equation that relates the rates.
Be certain not to substitute a variable quantity for ane of the variables until later finding an equation relating the rates.

For the following exercises, find the quantities for the given equation.

For the following exercises, sketch the situation if necessary and used related rates to solve for the quantities.

5.A 10 ft ladder is leaning against a wall. If the height of the ladder slides downwardly the wall at a rate of 2 ft/sec, how fast is the bottom moving along the ground when the bottom of the ladder is 5 ft from the wall?

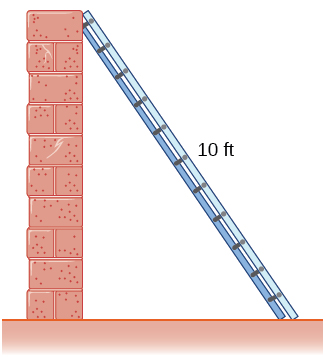
A right triangle is formed by a ladder leaning up against a brick wall. The ladder forms the hypotenuse and is 10 ft long.

Solution

$2\sqrt{3}$ ft/sec

6.A 25 ft ladder is leaning against a wall. If we button the ladder toward the wall at a rate of i ft/sec, and the bottom of the ladder is initially $20$ ft abroad from the wall, how fast does the ladder movement upwardly the wall $5$ sec subsequently we get-go pushing?

Solution

The distance is decreasing at $390$ mi/h.

8.You lot and a friend are riding your bikes to a restaurant that yous think is e; your friend thinks the eatery is north. You both get out from the same bespeak, with you riding at 16 mph east and your friend riding $12$ mph north. After yous traveled $4$ mi, at what rate is the distance betwixt you lot changing?

ix.Two buses are driving along parallel freeways that are $5$ mi apart, one heading e and the other heading w. Assuming that each passenger vehicle drives a abiding $55$ mph, discover the rate at which the distance between the buses is changing when they are $13$ mi apart, heading toward each other.

Solution

The altitude between them shrinks at a rate of $\frac{1320}{13}\approx 101.5$ mph.

10.A 6-ft-tall person walks away from a 10 ft lamppost at a constant charge per unit of $3$ ft/sec. What is the rate that the tip of the shadow moves away from the pole when the person is $10$ ft away from the pole?

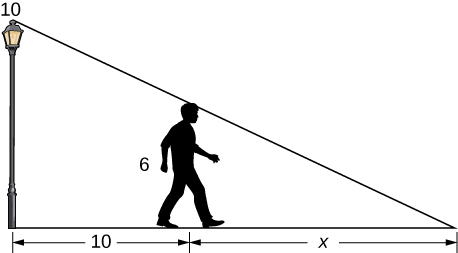
11.Using the previous problem, what is the rate at which the tip of the shadow moves away from the person when the person is 10 ft from the pole?

Solution

$\frac{9}{2}$ ft/sec

12.A 5-ft-tall person walks toward a wall at a rate of 2 ft/sec. A spotlight is located on the ground forty ft from the wall. How fast does the height of the person's shadow on the wall change when the person is 10 ft from the wall?

thirteen.Using the previous trouble, what is the rate at which the shadow changes when the person is x ft from the wall, if the person is walking away from the wall at a charge per unit of 2 ft/sec?

Solution

It grows at a rate $\frac{4}{9}$ ft/sec

14.A helicopter starting on the ground is rising directly into the air at a charge per unit of 25 ft/sec. Y'all are running on the footing starting directly under the helicopter at a rate of 10 ft/sec. Observe the rate of modify of the distance between the helicopter and yourself later 5 sec.

fifteen.Using the previous trouble, what is the charge per unit at which the distance between you and the helicopter is irresolute when the helicopter has risen to a height of lx ft in the air, assuming that, initially, it was 30 ft above yous?

Solution

The distance is increasing at $\frac{135\sqrt{26}}{26}$ ft/sec

For the post-obit exercises, draw and label diagrams to help solve the related-rates problems.

16.The side of a cube increases at a charge per unit of $\frac{1}{2}$ grand/sec. Notice the rate at which the volume of the cube increases when the side of the cube is 4 m.

17.The volume of a cube decreases at a charge per unit of 10 m/sec. Observe the rate at which the side of the cube changes when the side of the cube is ii thousand.

Solution

$-\frac{5}{6}$ m/sec

18.The radius of a circumvolve increases at a rate of 2 m/sec. Find the charge per unit at which the area of the circle increases when the radius is 5 m.

nineteen.The radius of a sphere decreases at a rate of 3 chiliad/sec. Observe the rate at which the surface surface area decreases when the radius is ten m.

Solution

$240\pi \, \text{m}^2$ /sec

20.The radius of a sphere increases at a rate of one 1000/sec. Find the charge per unit at which the volume increases when the radius is xx chiliad.

21.The radius of a sphere is increasing at a rate of 9 cm/sec. Find the radius of the sphere when the volume and the radius of the sphere are increasing at the same numerical rate.

Solution

$\frac{1}{2\sqrt{\pi}}$ cm

22.The base of a triangle is shrinking at a rate of 1 cm/min and the height of the triangle is increasing at a rate of 5 cm/min. Find the charge per unit at which the surface area of the triangle changes when the height is 22 cm and the base of operations is 10 cm.

23.A triangle has two constant sides of length iii ft and five ft. The angle between these two sides is increasing at a rate of 0.1 rad/sec. Detect the rate at which the area of the triangle is changing when the angle betwixt the 2 sides is $\pi /6$ .

Solution

The area is increasing at a rate $\frac{(3\sqrt{3})}{8} \, \text{ft}^{2} / \text{sec}$ .

24.A triangle has a height that is increasing at a rate of 2 cm/sec and its area is increasing at a charge per unit of 4 $\text{cm}^2 / \text{sec}$ . Find the rate at which the base of the triangle is changing when the peak of the triangle is 4 cm and the surface area is 20 $\text{cm}^2$ .

For the following exercises, consider a correct cone that is leaking water. The dimensions of the conical tank are a summit of 16 ft and a radius of 5 ft.

25.How fast does the depth of the water change when the h2o is 10 ft high if the cone leaks water at a rate of x $\text{ft}^3$ /min?

Solution

The depth of the water decreases at $\frac{128}{125\pi}$ ft/min.

26.Find the charge per unit at which the surface area of the water changes when the water is 10 ft high if the cone leaks h2o at a rate of 10 $\text{ft}^3$ /min.

27.If the h2o level is decreasing at a rate of 3 in./min when the depth of the water is 8 ft, determine the rate at which water is leaking out of the cone.

Solution

The volume is decreasing at a rate of $\frac{(25\pi )}{16}{\text{ft}}^{3}\text{/min}.$

28.A vertical cylinder is leaking water at a charge per unit of 1 $\text{ft}^3$ /sec. If the cylinder has a height of 10 ft and a radius of 1 ft, at what rate is the meridian of the h2o irresolute when the height is 6 ft?

29.A cylinder is leaking h2o merely you are unable to decide at what rate. The cylinder has a height of 2 m and a radius of 2 one thousand. Find the rate at which the water is leaking out of the cylinder if the charge per unit at which the tiptop is decreasing is 10 cm/min when the height is i m.

Solution

The water flows out at rate $\frac{2\pi}{5} \, \text{m}^3$ /min.

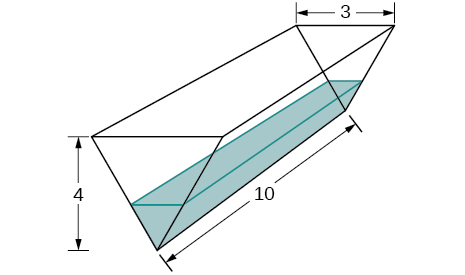
30.A trough has ends shaped like isosceles triangles, with width 3 m and height 4 m, and the trough is 10 g long. Water is being pumped into the trough at a rate of $5 \, \text{m}^3$ /min. At what charge per unit does the peak of the h2o change when the h2o is 1 m deep?

A trough is shown with ends shaped like isosceles triangles. These triangles have width 3 and height 4. The trough is made up of rectangles that are of length 10. There is some water in the trough.

31.A tank is shaped like an upside-downwards square pyramid, with base of operations of 4 m by 4 chiliad and a height of 12 m (see the post-obit effigy). How fast does the height increment when the water is ii m deep if h2o is beingness pumped in at a rate of $\frac{2}{3} \, \text{m}^3$ /sec?

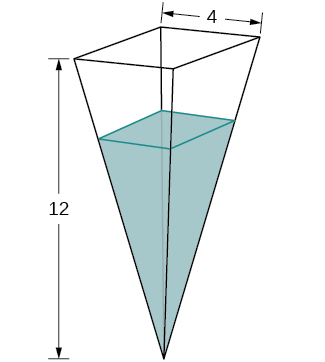
An upside-down square pyramid is shown with square side lengths 4 and height 12. There is an unspecified amount of water inside the shape.

Solution

$\frac{3}{2}$ m/sec

For the following problems, consider a pool shaped like the lesser half of a sphere, that is being filled at a rate of 25 $\text{ft}^3$ /min. The radius of the pool is 10 ft.

32.Find the rate at which the depth of the water is changing when the h2o has a depth of 5 ft.

33.Find the charge per unit at which the depth of the water is changing when the water has a depth of i ft.

Solution

$\frac{25}{19\pi}$ ft/min

34.If the height is increasing at a rate of 1 in/sec when the depth of the water is 2 ft, notice the rate at which water is being pumped in.

35.Gravel is being unloaded from a truck and falls into a pile shaped like a cone at a rate of x $\text{ft}^3$ /min. The radius of the cone base is iii times the height of the cone. Notice the charge per unit at which the height of the gravel changes when the pile has a summit of five ft.

Solution

$\frac{2}{45\pi}$ ft/min

36.Using a similar setup from the preceding problem, observe the charge per unit at which the gravel is beingness unloaded if the pile is 5 ft loftier and the height is increasing at a rate of 4 in/min.

For the following exercises, draw the situations and solve the related-rate problems.

37.You are stationary on the ground and are watching a bird fly horizontally at a rate of 10 m/sec. The bird is located 40 m above your head. How fast does the angle of elevation modify when the horizontal distance betwixt y'all and the bird is 9 m?

Solution

The bending decreases at $\frac{400}{1681}$ rad/sec.

38.You stand 40 ft from a bottle rocket on the ground and lookout man as it takes off vertically into the air at a rate of twenty ft/sec. Find the rate at which the angle of tiptop changes when the rocket is thirty ft in the air.

39.A lighthouse, $L$ , is on an isle 4 mi away from the closest betoken, $P$ , on the beach (see the following prototype). If the lighthouse light rotates clockwise at a constant rate of ten revolutions/min, how fast does the beam of calorie-free move across the beach 2 mi abroad from the closest point on the beach?

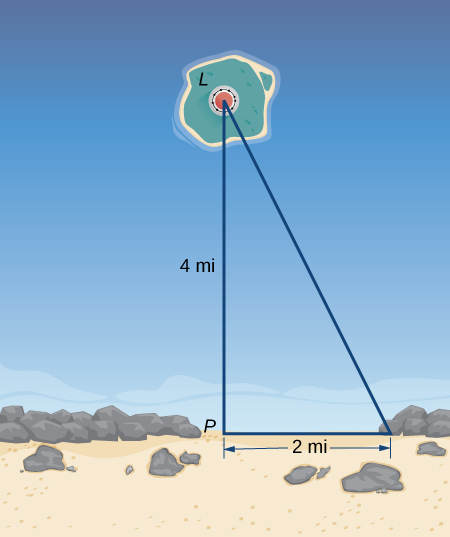
A right triangle is formed by a lighthouse L, a point P on the shore that is perpendicular to the line from the lighthouse to the shore, and a point 2 miles to the right of the point P. The distance from P to L is 4 miles.

Solution

$100\pi$ mi/min

40.Using the same setup as the previous trouble, make up one's mind at what rate the axle of lite moves across the beach 1 mi abroad from the closest betoken on the beach.

41.You are walking to a motorcoach end at a right-angle corner. You motion due north at a rate of 2 k/sec and are 20 1000 south of the intersection. The bus travels west at a rate of ten 1000/sec abroad from the intersection – you have missed the bus! What is the rate at which the bending between y'all and the bus is changing when you are 20 m south of the intersection and the bus is 10 g w of the intersection?

Solution

The angle is changing at a rate of $\frac{21}{25}$ rad/sec.

For the following exercises, refer to the figure of baseball diamond, which has sides of 90 ft.

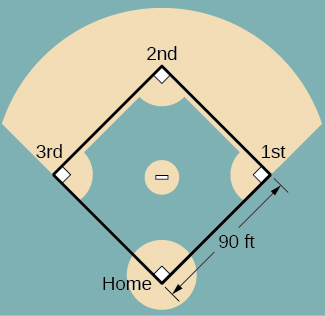
A baseball field is shown, with the bases labeled Home, 1st, 2nd, and 3rd making a square with side lengths 90 ft.

42. [T] A batter hits a brawl toward 3rd base at 75 ft/sec and runs toward first base at a rate of 24 ft/sec. At what rate does the altitude between the ball and the concoction change when 2 sec have passed?

43. [T] A concoction hits a brawl toward second base of operations at 80 ft/sec and runs toward offset base at a rate of 30 ft/sec. At what rate does the distance between the ball and the batter alter when the runner has covered one-tertiary of the distance to outset base? (Hint: Call back the law of cosines.)

Solution

The altitude is increasing at a rate of 62.l ft/sec.

44. [T] A batter hits the ball and runs toward start base at a speed of 22 ft/sec. At what rate does the distance between the runner and 2nd base change when the runner has run 30 ft?

45. [T] Runners kickoff at first and second base. When the baseball is hit, the runner at commencement base of operations runs at a speed of xviii ft/sec toward second base of operations and the runner at second base of operations runs at a speed of 20 ft/sec toward 3rd base of operations. How fast is the distance between runners irresolute i sec after the brawl is striking?

Solution

The distance is decreasing at a rate of 11.99 ft/sec.

Glossary

related rates: are rates of change associated with two or more related quantities that are changing over fourth dimension

Source: https://opentextbc.ca/calculusv1openstax/chapter/related-rates/

Posted by: smileyfres1968.blogspot.com

At What Rate Is The Exposed Surface Area Of The Water Changing When The Radius Is 2 Feet

iv.1 Related Rates

Learning Objectives

Setting upward Related-Rates Problems

Inflating a Balloon

Solution

Solution

Problem-Solving Strategy: Solving a Related-Rates Trouble

Examples of the Procedure

An Plane Flying at a Constant Top

Solution

Solution

Chapter Opener: A Rocket Launch

Solution

Solution

H2o Draining from a Funnel

Solution

Solution

Key Concepts

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Solution

Glossary

0 Response to "At What Rate Is The Exposed Surface Area Of The Water Changing When The Radius Is 2 Feet"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel